Shik給我的一個既痛苦又快樂的禮物
有一些東西需要證明,麻煩的要命
而且我覺得還蠻難想到要怎麼做的
雖然一看就覺得是D&C,但我還是卡了很久
其實我本來想要找的就是對每個點距離最近的點
一開始想要使用最近點對的那種概念
亂想有些地方沒想清楚直接就開始coding了
後來才發現根本有誤,一切並沒有這麼簡單
因為有可能根本無法構成一棵樹
這時我就決定只要向右的最近點對就好了,但是還是不行
但是也有越來越接近答案的趨勢了
正解: 4* ( D&C ) -> Kruskal
看右上跟右下也還是不行,必須要分成八塊去看(對於每個點都選最近的)
PROOF: 假定有一生成樹包含e,這時有一個點w,比 v 更靠近 u 。若把 e 這個邊拿掉,則此生成樹會變成兩個,而 w 有可能跟 u 在一起(d(w,v) < d(u,v)) or 跟 v 在一起(d(u,w) < d(u,v)),無論何種情況,都會比v還要好,所以每一個octant都只要選一個最近的就好了。(如果是quadrant的話就沒有辦法這麼證了,所以分四份是不行的)
但是基於在思考右上右下的時候,發現的一個規則,也可以在這裡使用到。
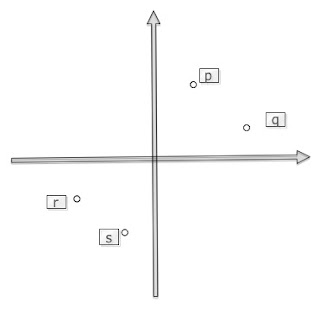
當p, q都在r, s的右上角,若且唯若 d( p, r ) < d( q, r ),則 d( p, s ) < d( q, s )。
PROOF: px-rx+py-ry < qx-rx+qy-ry <-> px+py < qx+qy <-> px-sx+py-sy < qx-sx+qy-sy
有了這個性質,就可以用D&C以 O(nlgn) 的時間找出每一個點左上方的最近點為何。而在做D&C的時候,可以O(n)合併,雙指標,一個指左邊,一個指右邊,用著我剛剛說的性質,邊跑邊sort Y座標。
最後最重要的就是怎麼把上述兩種作法結合成一個,而這就要用到強大的數學?!
巧妙的做座標轉換:
右上上:( a, b ) -> ( b-a, 2a )
右上右:( a, b ) -> ( a-b, 2b )
右下右:( a, b ) -> ( a+b, -2b )
右下下:( a, b ) -> ( -a-b, 2a )
如此就可以看到那四塊區域,然後又可以使用那個找左上角的D&C作法。
code: http://codepad.org/X4ZPZ5BE

沒有留言:
張貼留言