其實我本來看不懂題目的==
敘述有點怪怪的+ +
後來原來是要叫我們找AP
就用,dfn 跟 low一次解決
最下面的點:不行(不是會產生迴圈就是沒有下面的節點)
中間的點:如果有子節點可以走到上面不行(會產生迴圈)
最上面的點:如果只有一顆子樹不行(就跟最下面的點一樣)
SO::
若沒有子節點-> 不行
若全部子節點都走到上面-> 不行
若為root且子樹少於2 -> 不行
code: http://codepad.org/FOPjxS0v
2012年5月31日 星期四
2012年5月30日 星期三
tioj 1078 陽數
沒有很難,純粹想要有較多的code在我的blog裡
暴力+排組(nCm 先建立好表格 -> 50 * 50)
不難,雖然剛升高一時,完全不會?!
現在想起來還挺納悶的,大概是不會排組的關係吧
喔,但是有點複雜,有小細節要寫好
code: http://codepad.org/iuKEsOPV
暴力+排組(nCm 先建立好表格 -> 50 * 50)
不難,雖然剛升高一時,完全不會?!
現在想起來還挺納悶的,大概是不會排組的關係吧
喔,但是有點複雜,有小細節要寫好
code: http://codepad.org/iuKEsOPV
2012年5月27日 星期日
tioj 1500 Clean up on aisle 3
極裸最近點對
不是太難寫,但是要注意浮點數誤差
我太不常寫麻煩題了,常常沒有注意到
作法就是你想的那樣
1. 依 x 座標排序
2. 找出左半邊的跟右半邊的最小值
3. T(6*n) 找出跨兩邊的最小值
4. 用 Merge sort 排序
code: http://codepad.org/tZW0KF6J
不是太難寫,但是要注意浮點數誤差
我太不常寫麻煩題了,常常沒有注意到
作法就是你想的那樣
1. 依 x 座標排序
2. 找出左半邊的跟右半邊的最小值
3. T(6*n) 找出跨兩邊的最小值
4. 用 Merge sort 排序
code: http://codepad.org/tZW0KF6J
2012年5月26日 星期六
tioj 1208 第K大連續和
二分搜答案 -> MergeSort求有多少個大於此答案
Merge Sort 那邊不太難,自己想(用雙指標,跟普通的Merge Sort差不多)
重點是二分搜答案的部份!!很容易沒想清楚TLE!!
這裡要來好好分析一下二分搜,不要再亂用猜的方式去寫答案
1. 最基本的:
while( lb < rb ){
int mid = ( lb + rb ) / 2;
if( ... ) lb = mid+1;
else rb = mid;
}
想法:每次都減少範圍,直到 lb == rb。(... 為答案不可能是 mid 的情況)
證明:
當 rb - lb > 1時,rb >= lb+2,故mid >= lb+1(且mid < rb)
若情況為if,則範圍變小。若情況為else,則範圍亦變小。
當 rb - lb == 1 時,若 0 <= lb,則mid = lb,不管如何範圍都變小。
但若 lb < 0,則mid = rb,有可能範圍是不會變小的。(也就會引到TLE)
2. 較複雜的:
while( lb < rb-1 ){
int mid = ( lb + rb ) / 2;
if( ... ) lb = mid;
else rb = mid;
}
想法:rb 是指向最上界 + 1(... 為答案不可能是 mid 的情況)
證明:
當 rb - lb > 1時,一切都跟最基本的證明相同,無論如何範圍都會變小。
但是 rb 不會等於 lb+1,所以下面會引到TLE的點不存在,故不會引到TLE。
我的code:http://codepad.org/Gxh07Lzj
Merge Sort 那邊不太難,自己想(用雙指標,跟普通的Merge Sort差不多)
重點是二分搜答案的部份!!很容易沒想清楚TLE!!
這裡要來好好分析一下二分搜,不要再亂用猜的方式去寫答案
1. 最基本的:
while( lb < rb ){
int mid = ( lb + rb ) / 2;
if( ... ) lb = mid+1;
else rb = mid;
}
想法:每次都減少範圍,直到 lb == rb。(... 為答案不可能是 mid 的情況)
證明:
當 rb - lb > 1時,rb >= lb+2,故mid >= lb+1(且mid < rb)
若情況為if,則範圍變小。若情況為else,則範圍亦變小。
當 rb - lb == 1 時,若 0 <= lb,則mid = lb,不管如何範圍都變小。
但若 lb < 0,則mid = rb,有可能範圍是不會變小的。(也就會引到TLE)
2. 較複雜的:
while( lb < rb-1 ){
int mid = ( lb + rb ) / 2;
if( ... ) lb = mid;
else rb = mid;
}
想法:rb 是指向最上界 + 1(... 為答案不可能是 mid 的情況)
證明:
當 rb - lb > 1時,一切都跟最基本的證明相同,無論如何範圍都會變小。
但是 rb 不會等於 lb+1,所以下面會引到TLE的點不存在,故不會引到TLE。
我的code:http://codepad.org/Gxh07Lzj
2012年5月23日 星期三
tioj 1645 電路啟動方案
這是為了慶祝我即將到達300題
Shik給我的一個既痛苦又快樂的禮物
有一些東西需要證明,麻煩的要命
而且我覺得還蠻難想到要怎麼做的
雖然一看就覺得是D&C,但我還是卡了很久
其實我本來想要找的就是對每個點距離最近的點
一開始想要使用最近點對的那種概念
亂想有些地方沒想清楚直接就開始coding了
後來才發現根本有誤,一切並沒有這麼簡單
因為有可能根本無法構成一棵樹
這時我就決定只要向右的最近點對就好了,但是還是不行
但是也有越來越接近答案的趨勢了
正解: 4* ( D&C ) -> Kruskal
看右上跟右下也還是不行,必須要分成八塊去看(對於每個點都選最近的)
PROOF: 假定有一生成樹包含e,這時有一個點w,比 v 更靠近 u 。若把 e 這個邊拿掉,則此生成樹會變成兩個,而 w 有可能跟 u 在一起(d(w,v) < d(u,v)) or 跟 v 在一起(d(u,w) < d(u,v)),無論何種情況,都會比v還要好,所以每一個octant都只要選一個最近的就好了。(如果是quadrant的話就沒有辦法這麼證了,所以分四份是不行的)
但是基於在思考右上右下的時候,發現的一個規則,也可以在這裡使用到。
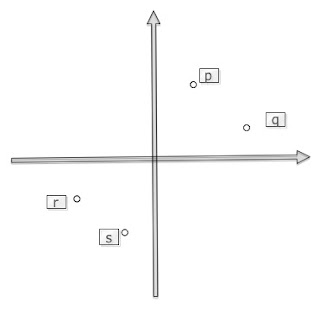
當p, q都在r, s的右上角,若且唯若 d( p, r ) < d( q, r ),則 d( p, s ) < d( q, s )。
PROOF: px-rx+py-ry < qx-rx+qy-ry <-> px+py < qx+qy <-> px-sx+py-sy < qx-sx+qy-sy
如此就可以看到那四塊區域,然後又可以使用那個找左上角的D&C作法。
code: http://codepad.org/X4ZPZ5BE
Shik給我的一個既痛苦又快樂的禮物
有一些東西需要證明,麻煩的要命
而且我覺得還蠻難想到要怎麼做的
雖然一看就覺得是D&C,但我還是卡了很久
其實我本來想要找的就是對每個點距離最近的點
一開始想要使用最近點對的那種概念
亂想有些地方沒想清楚直接就開始coding了
後來才發現根本有誤,一切並沒有這麼簡單
因為有可能根本無法構成一棵樹
這時我就決定只要向右的最近點對就好了,但是還是不行
但是也有越來越接近答案的趨勢了
正解: 4* ( D&C ) -> Kruskal
看右上跟右下也還是不行,必須要分成八塊去看(對於每個點都選最近的)
PROOF: 假定有一生成樹包含e,這時有一個點w,比 v 更靠近 u 。若把 e 這個邊拿掉,則此生成樹會變成兩個,而 w 有可能跟 u 在一起(d(w,v) < d(u,v)) or 跟 v 在一起(d(u,w) < d(u,v)),無論何種情況,都會比v還要好,所以每一個octant都只要選一個最近的就好了。(如果是quadrant的話就沒有辦法這麼證了,所以分四份是不行的)
但是基於在思考右上右下的時候,發現的一個規則,也可以在這裡使用到。
當p, q都在r, s的右上角,若且唯若 d( p, r ) < d( q, r ),則 d( p, s ) < d( q, s )。
PROOF: px-rx+py-ry < qx-rx+qy-ry <-> px+py < qx+qy <-> px-sx+py-sy < qx-sx+qy-sy
有了這個性質,就可以用D&C以 O(nlgn) 的時間找出每一個點左上方的最近點為何。而在做D&C的時候,可以O(n)合併,雙指標,一個指左邊,一個指右邊,用著我剛剛說的性質,邊跑邊sort Y座標。
最後最重要的就是怎麼把上述兩種作法結合成一個,而這就要用到強大的數學?!
巧妙的做座標轉換:
右上上:( a, b ) -> ( b-a, 2a )
右上右:( a, b ) -> ( a-b, 2b )
右下右:( a, b ) -> ( a+b, -2b )
右下下:( a, b ) -> ( -a-b, 2a )
如此就可以看到那四塊區域,然後又可以使用那個找左上角的D&C作法。
code: http://codepad.org/X4ZPZ5BE
2012年5月20日 星期日
tioj 1752 Ch1. Section 2. 妹妹的汽水
題目敘述好複雜,多看了幾眼之後
其實他在做的就只是把最大的移到最後面罷了
而他又是從2,3,5,7這樣移下去
那你就依序從2,3,5,7的最大一個一個刪去
(只要刪到n^(1/2)就好了)
最後得到的就是答案啦(當然要順便歸零啦)
這樣時間複雜度O( n^(1/2) * T ),恰好1 sec
阿題目有BUG,1也要當成質數,害我一直WA
http://codepad.org/F7fzCE2i
其實他在做的就只是把最大的移到最後面罷了
而他又是從2,3,5,7這樣移下去
那你就依序從2,3,5,7的最大一個一個刪去
(只要刪到n^(1/2)就好了)
最後得到的就是答案啦(當然要順便歸零啦)
這樣時間複雜度O( n^(1/2) * T ),恰好1 sec
阿題目有BUG,1也要當成質數,害我一直WA
http://codepad.org/F7fzCE2i
tioj 1757 Ch2. Section 2. 危險的樓梯間
今天遇見了一個我一直以為我不會遇見的東西
-> 循環節
先來證明費氏數列擁有循環節好了
餘數系:A = { 0, 1, 2, 3, ... k-1 } (mod k)
設定{ ( x, y ) , x 屬於 A 且 y 屬於 A },有k*k種組合
所以在 k^2 項之內一定會出現重複
而且 Fn = Fn-1 + Fn-2
所以當( i, i+1 ) 和 ( j, j+1 ) 一樣時,i+2 = j+2 且 i-1 = j-1
意味著每距離 j-i ,就會出現跟自己一樣的
因此費氏數列有循環節。
至於這個距離,據說是沒有辦法計算出來的,
你可以直接假定初始的兩項,再 dp 跑過去
找到跟初始一樣的兩項即找到距離
這提用矩陣累乘配合循環節,即可成功AC囉!
http://codepad.org/uDwR2UAT
-> 循環節
先來證明費氏數列擁有循環節好了
餘數系:A = { 0, 1, 2, 3, ... k-1 } (mod k)
設定{ ( x, y ) , x 屬於 A 且 y 屬於 A },有k*k種組合
所以在 k^2 項之內一定會出現重複
而且 Fn = Fn-1 + Fn-2
所以當( i, i+1 ) 和 ( j, j+1 ) 一樣時,i+2 = j+2 且 i-1 = j-1
意味著每距離 j-i ,就會出現跟自己一樣的
因此費氏數列有循環節。
至於這個距離,據說是沒有辦法計算出來的,
你可以直接假定初始的兩項,再 dp 跑過去
找到跟初始一樣的兩項即找到距離
這提用矩陣累乘配合循環節,即可成功AC囉!
http://codepad.org/uDwR2UAT
2012年5月17日 星期四
tioj 1711 Apple Tree [完成]
很久以前就想寫這題了
最近想了一個 O(n^3) 的作法,是引用了樹型DP的概念
可惜時間複雜度還是不對,co了還是TLE
雖然覺得方向沒錯,但卻一直想不到O(n^2)或O(n^2logn)
我後來是用一些怪異的優化才AC的,真的是不太漂亮
但卻完全想不到好作法 = =,有寄信去問學長
後來學長用很神祕的解釋方法使我了解他應該是O( n^2 )
我來說一下我的作法好了
首先從root開始DFS:
對於每一個子樹遞迴後,測試:
1. 走一段路後到那個子樹然後回到當下節點
2. 走一段路後到那個子樹然後就不回來了
3. 先去那個子樹再走一段路然後回到當下節點
[ 每一種步數 * 每一種步數分配 = O(n) ] *(O(n) -> 每一個節點)= O( n^2 )
其實要解一個奇怪的方程式吧,就像D&C講義寫的那樣,可是我不會XD
樂正學長的解釋:
O(n^2)作法:http://codepad.org/4aQpqTWP
最近想了一個 O(n^3) 的作法,是引用了樹型DP的概念
可惜時間複雜度還是不對,co了還是TLE
雖然覺得方向沒錯,但卻一直想不到O(n^2)或O(n^2logn)
我後來是用一些怪異的優化才AC的,真的是不太漂亮
但卻完全想不到好作法 = =,有寄信去問學長
後來學長用很神祕的解釋方法使我了解他應該是O( n^2 )
我來說一下我的作法好了
首先從root開始DFS:
對於每一個子樹遞迴後,測試:
1. 走一段路後到那個子樹然後回到當下節點
2. 走一段路後到那個子樹然後就不回來了
3. 先去那個子樹再走一段路然後回到當下節點
[ 每一種步數 * 每一種步數分配 = O(n) ] *(O(n) -> 每一個節點)= O( n^2 )
其實要解一個奇怪的方程式吧,就像D&C講義寫的那樣,可是我不會XD
樂正學長的解釋:
最差情況似乎不會超過O(n^2) 平衡2元樹T(n)=2T(n/2)+(n/2)*(n/2)=2T(n/2)+O(n^2) 平衡3元樹T(n)=3T(n/3)+(n/3)*(n/3)+(2n/3)*(n/3)=2T(n/2)+O(n^2) 平衡4元樹T(n)=4T(n/4)+(n/4)*(n/4)+(2n/4)*(n/4)+(3n/4)*(n/4)=2T(n/2)+O(n^2) 鏈狀T(n)=T(n-1)+O(n)
O(n^2)作法:http://codepad.org/4aQpqTWP
tioj 1711 山洞
矩陣累乘
因為當下狀態只受最後兩排影響
且這兩排有69種組合
我就開了69*69的矩陣
我的排列矩陣中,只有第一排是有用的,其餘都是廢物
初始矩陣:i=1~69, j=1 ( 1 ),i=1~69, j=2~69 ( 0 )
-> 代表最後兩排第 1 種~第69種都有一種排法
遞移矩陣:要用程式跑,先跑完才開始做累乘
-> mat[i][j]=0 代表第 i 種會被第 j 種卡到
然後用快速冪logn求出答案
http://codepad.org/GTV5gZmu
因為當下狀態只受最後兩排影響
且這兩排有69種組合
我就開了69*69的矩陣
我的排列矩陣中,只有第一排是有用的,其餘都是廢物
初始矩陣:i=1~69, j=1 ( 1 ),i=1~69, j=2~69 ( 0 )
-> 代表最後兩排第 1 種~第69種都有一種排法
遞移矩陣:要用程式跑,先跑完才開始做累乘
-> mat[i][j]=0 代表第 i 種會被第 j 種卡到
然後用快速冪logn求出答案
http://codepad.org/GTV5gZmu
tioj 1707 奶牛計算機
先用stack,再用queue
stack: 求每個運算符號對應到的割點(不是真的割點)
從後面做回來,碰到運算子就push,碰到變數就 a[top]->變數位置, pop
queue: 依照規則,回推回原本的狀況
分成兩半,分別push,一直分下去,直到無法在分兩半
http://codepad.org/aOfCDqpZ
2012年5月12日 星期六
tioj 1706 烏龜暗殺
題目很複雜,要多想一下下
題目敘述:
給你一個有向圖上每個邊權重的截距與斜率
要你找一天使得從起點到終點再回起點的權重和最小
剛想的時候,會覺得很困難
但多想一下,就會發現得到的答案一定會是 ( 某些權重和 + 某些斜率和 * Day )
於是盲點就破解了
若斜率和 > 0,Day = 0
否則,Day = maximum day( -> D )
所以就做兩次Dijkstra,一次是Day 0,一次是Day D,取 min
http://codepad.org/qepmJf30
題目敘述:
給你一個有向圖上每個邊權重的截距與斜率
要你找一天使得從起點到終點再回起點的權重和最小
剛想的時候,會覺得很困難
但多想一下,就會發現得到的答案一定會是 ( 某些權重和 + 某些斜率和 * Day )
於是盲點就破解了
若斜率和 > 0,Day = 0
否則,Day = maximum day( -> D )
所以就做兩次Dijkstra,一次是Day 0,一次是Day D,取 min
http://codepad.org/qepmJf30
訂閱:
意見 (Atom)